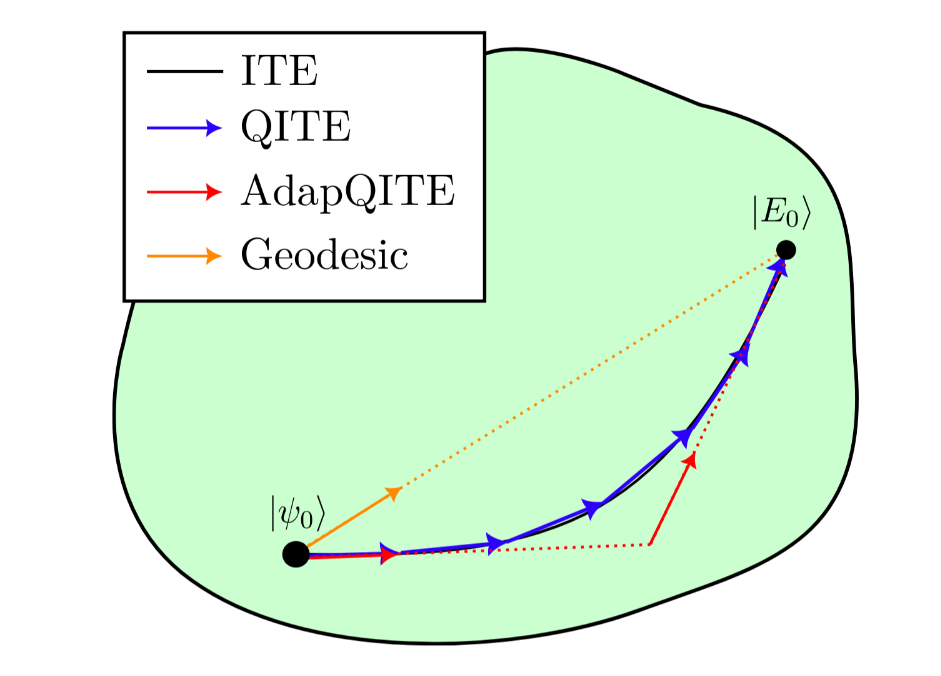
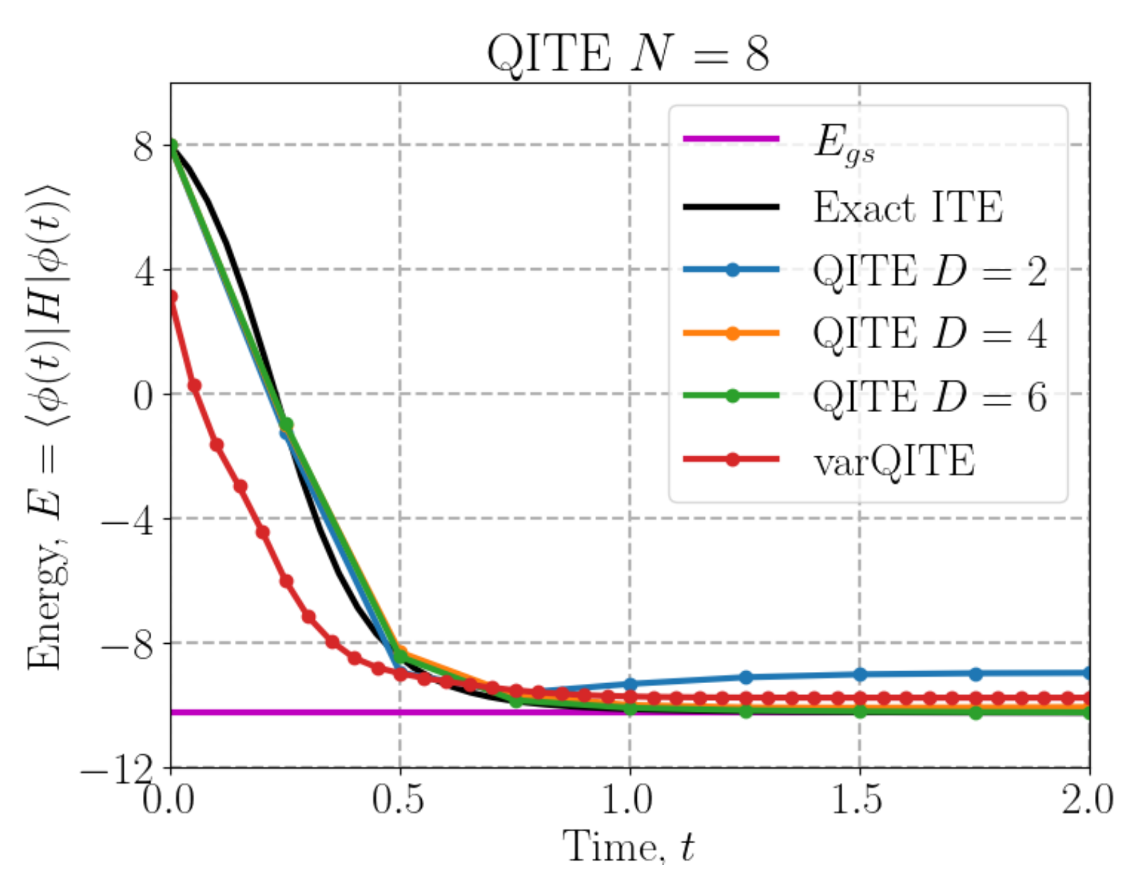
Preparing the ground state of a given Hamiltonian is a computational task of interest in many fields, such as material science, chemistry and even some optimization problems, to name a few. Efficiently preparing ground states for large, strongly correlated systems is a challenging task for both classical and quantum hardware. Drawing from classical optimization methods, e.g. dynamical optimization techniques, one may deduce the spectral decomposition in manner that avoids direct spectral decomposition and is amenable to Trotterization methods. An instance of the latter is ground state preparation by Imaginary Time Evolution (ITE), understood in physical terms as a natural cooling process. Its quantum version QITE (Quantum Imaginary Time Evolution) aims at implementing ITE in a quantum computer. In this paper we introduce a novel QITE algorithm, which leverages underlying geometric properties for algorithm-runtime and circuit depth reduction. This will materialize in the form of an iterative Line Search approach for minimization of energy as well as a Newton's method approach for the deduction of the optimal time-steps for each iteration of QITE. The depth-reduction will be carried out via approximating the resulting unitary operator estimated from the QITE algorithm with unitary operator which is an element of a one-parameter group; making expressible as a single unitary in a quantum circuit. Furthermore, we perform a numerical study to stablish the scaling of fidelities with the different truncation parameters and give gate counts estimates for each. ···

We study a one-dimensional frustrated spin chain, which combines cluster-Ising and anisotropic next-nearest neighbor Ising models. We first offer a historical perspective that justifies the studied model. Then we study in detail the two quantum phases and prove that they are separated by a first order quantum phase transition. On one side, the ground state corresponds to a ferromagnetic phase, shows the presence of macroscopic cat states, and a small gap that closes in the thermodynamic limit. On the other phase, competing interactions avoid the establishment of a topological phase, though it conserves large incommensurate quantum correlations. We prove it is fundamentally distinct from a simple paramagnet, and we name it an incommensurate phase. This is a gapped phase, which gap does not close in the thermodynamic limit. While in the ferromagnetic phase there are two dominant Schmidt coefficients, in the incommensurate phase there are four. This corresponds to four distinct bipartite entanglement channels contributing substantially to the ground state. Finally, we discuss the utility of the macroscopic cat states for quantum metrology applications and the experimental feasibility of the system. ···

Ansatz selection is a key factor in the performance of variational quantum algorithms (VQAs). While much of the state-of-the-art still relies on heuristic choices, an inadequate circuit structure can compromise both the expressive power and the trainability of the resulting model. Recent results have also established theoretical connections between expressibility and the onset of barren plateaus, highlighting the need for systematic criteria for ansatz selection. In this work, the ansatz is treated as a design feature to be optimized rather than a fixed block, and a design space exploration (DSE) is performed over a diverse set of parametrized quantum circuits (PQCs). Three complementary metrics -- expressibility, trainability, and resource cost -- are evaluated and used to analyze the trade-offs that emerge across different PQCs. Beyond identifying Pareto-optimal candidates, this multi-objective perspective helps clarify the interplay between these metrics and contributes quantitative evidence toward understanding the expressibility--trainability tension in variational circuits. ···

Trapped-ion Quantum Charge-Coupled Device (QCCD) architectures promise scalability through interconnected trap zones and dynamic ion transport; however, this transport capability creates a complex compilation challenge: how to move qubits efficiently without degrading fidelity. We introduce a routing strategy that turns this challenge into an advantage by exploiting operational parallelism across traps while adapting to both algorithmic structure and device topology through a configurable multi-parameter scoring mechanism. Across a broad suite of benchmarks and QCCD layouts, the method consistently reduces ion-transport overhead and improves execution fidelity, outperforming state-of-the-art routing techniques. These results highlight that explicitly balancing movement overhead and execution parallelism under architectural constraints is key to unlocking the full potential of modular trapped-ion quantum processors. ···

Many computationally hard problems can be encoded in quantum Hamiltonians. The solution to these problems is given by the ground states of these Hamiltonians. A state-of-the-art algorithm for finding the ground state of a Hamiltonian is the so-called Quantum Imaginary Time Evolution (QITE) which approximates imaginary time evolution by a unitary evolution that can be implemented in quantum hardware. In this paper, we review the original algorithm together with a comprehensive computer program, as well as, the variational version of it. ···

We propose a nonlinear quantum walk model inspired in a photonic implementation in which the polarization state of the light field plays the role of the coin-qubit. In particular, we take profit of the nonlinear polarization rotation occurring in optical media with Kerr nonlinearity, which allows to implement a nonlinear coin operator, one that depends on the state of the coin-qubit. In particular, we observe that the probability distribution becomes, at large time steps, concentrated near the "low energy" brane, and can be approximated as the lowest eigenstate of the continuum Hamiltonian that is compatible with the symmetries of the model. In this way, we obtain a localization effect whose strength is controlled by a warp coefficient. In other words, here localization arises from the geometry of the model, at variance with the usual effect that is originated from random irregularities, as in Anderson localization. In summary, we establish an interesting correspondence between a high energy physics model and localization in quantum walks. ···

We investigate the properties of a quantum walk which can simulate the behavior of a spin $1/2$ particle in a model with an ordinary spatial dimension, and one extra dimension with warped geometry between two branes. Such a setup constitutes a $1+1$ dimensional version of the Randall-Sundrum model, which plays an important role in high energy physics. In the continuum spacetime limit, the quantum walk reproduces the Dirac equation corresponding to the model, which allows to anticipate some of the properties that can be reproduced by the quantum walk. In particular, we observe that the probability distribution becomes, at large time steps, concentrated near the "low energy" brane, and can be approximated as the lowest eigenstate of the continuum Hamiltonian that is compatible with the symmetries of the model. In this way, we obtain a localization effect whose strength is controlled by a warp coefficient. In other words, here localization arises from the geometry of the model, at variance with the usual effect that is originated from random irregularities, as in Anderson localization. In summary, we establish an interesting correspondence between a high energy physics model and localization in quantum walks. ···

In this paper, we present steady-state relativistic magnetohydrodynamic simulations that include a mass-load term to study the process of jet deceleration. The mass load mimics the injection of a proton–electron plasma from stellar winds within the host galaxy into initially pair plasma jets, with mean stellar mass-losses ranging from $10^{-14}$ to $10^{-9}\,{M_\odot\,yr^{-1}}$⁠. The spatial jet evolution covers ∼ 500pc from jet injection in the grid at 10 pc from the jet nozzle. Our simulations use a relativistic gas equation of state and a pressure profile for the ambient medium. We compare these simulations with previous dynamical simulations of relativistic, non-magnetized jets. Our results show that toroidal magnetic fields can prevent fast jet expansion and the subsequent embedding of further stars via magnetic tension. In this sense, magnetic fields avoid a runaway deceleration process. Furthermore, when the mass load is large enough to increase the jet density and produce fast, differential jet expansion, the conversion of magnetic energy flux into kinetic energy flux (i.e. magnetic acceleration), helps to delay the deceleration process with respect to non-magnetized jets. We conclude that the typical stellar population in elliptical galaxies cannot explain jet deceleration in classical Fanaroff–Riley type I radio galaxies. However, we observe a significant change in the jet composition, thermodynamical parameters, and energy dissipation along its evolution, even for moderate values of the mass load. ···

The usual paradigm of open quantum systems falls short when the environment is actually coupled to additional fields or components that drive it out of equilibrium. Here we explore the simplest such scenario, by considering a two level system coupled to a first thermal reservoir that in turn couples to a second thermal bath at a different temperature. We derive a master equation description for the system and show that, in this situation, the dynamics can be especially rich. In particular, we observe prethermalization, a transitory phenomenon in which the system initially approaches thermal equilibrium with respect to the first reservoir, but after a longer time converges to the thermal state dictated by the temperature of the second environment. Using analytical arguments and numerical simulations, we analyze the occurrence of this phenomenon, and how it depends on temperatures and coupling strengths. The phenomenology gets even richer if the system is placed between two such non-equilibrium environments. In this case, the energy current through the system may exhibit transient features and even switch direction, before the system eventually reaches a non-equilibrium steady state.···

Two models are first presented, of one-dimensional discrete-time quantum walk (DTQW) with temporal noise on the internal degree of freedom (i.e., the coin): (i) a model with both a coin-flip and a phase-flip channel, and (ii) a model with random coin unitaries. It is then shown that both these models admit a common limit in the spacetime continuum, namely, a Lindblad equation with Dirac-fermion Hamiltonian part and, as Lindblad jumps, a chirality flip and a chirality-dependent phase flip, which are two of the three standard error channels for a two-level quantum system. This, as one may call it, Dirac Lindblad equation, provides a model of quantum relativistic spatial diffusion, which is evidenced both analytically and numerically. This model of spatial diffusion has the intriguing specificity of making sense only with original unitary models which are relativistic in the sense that they have chirality, on which the noise is introduced: The diffusion arises via the by-construction (quantum) coupling of chirality to the position. For a particle with vanishing mass, the model of quantum relativistic diffusion introduced in the present work, reduces to the well-known telegraph equation, which yields propagation at short times, diffusion at long times, and exhibits no quantumness. Finally, the results are extended to temporal noises which depend smoothly on position.···